Задача
Исследуйте, сколько решений имеет система уравнений
x² + y² + xy = a,
x² – y² = b,
где а и b – некоторые данные действительные числа.
Решение
Перейдём к новым переменным: x + y = u, x – y = v. Тогда система запишется так: 3u² + v² = 4a², uv = b . (*)
Очевидно, что каждой паре (x, y) соответствует одна пара (u, v) , а каждой паре (u, v) – пара (x, y), так что нам нужно выяснить, сколько решений при различных значениях параметров a и b имеет система (*).
Вычтем и прибавим к первому уравнению системы (*) второе уравнение,
умноженное на 
Получим:
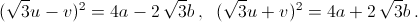
Остается учесть, что уравнение z² = c имеет два решения, если c > 0, одно, если c = 0, и не имеет решений, если c < 0.
Ответ
Решения есть тогда и только тогда, когда выполнены неравенства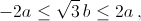 
причём, если оба неравенства строгие ("меньше"), то решений четыре; если одно из них обращается в равенство – то два, если оба (это возможно лишь при a = b = 0, то одно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь