Задача
а) Докажите, что в таблице
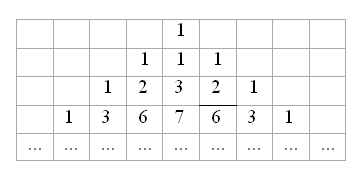
Решение
а) Будем в нашей таблице вместо чётных чисел писать 0, а вместо нечётных – 1. Тогда таблицу из нулей и единиц нужно будет составлять по тому же правилу (каждое число получается как сумма трёх, стоящих над ним в предыдущей строке), только сложение нужно выполнять по модулю два.
Первый способ. Последние четыре числа в каждой строке зависят только от того, каковы последние четыре числа в предыдущей строке, поэтому эта четвёрка периодически повторяется (с периодом 4, см. рис. 1).
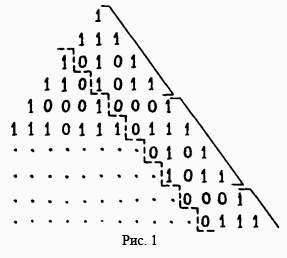
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет