Пусть A₁ и B₁ – середины диагоналей AC и BD трапеции, E и F – середины боковых сторон AD и BC (рис.2). Поскольку A₁ F – средняя линия треугольника ACB , a B₁ F – средняя линия треугольника DCB , то точки A₁ и B₁ лежат на отрезке EF и

a₁=A₁ B₁=|A₁ F-B₁ F|=||.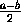

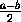(Эта формула верна независимо от того, какое из чисел a и b больше). Точно так же доказывается, что где a_n=A_n B_n (n=1,2,3, ...)– интересующая нас последовательность. Тем самым задача сведена к чисто алгебраической задаче о последовательности, определяемой соотношением(eq97.1) с начальным членом a₀=a>0.

Если a_n>b , то a_n+1=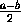<a_n-b . Поэтому если a>b , то каждый член последовательности будет меньше предыдущего по крайней мере на b до тех пор, пока не встретится член a_m такой, что a_m b (если a b , то положим m=0, a_m=a₀=a ; многие читатели рассматривали только этот случай; только он рассматривается и в книге "Математические задачи" (Е.Б.Дынкин, С.А.Молчанов, А.Л.Розенталь, А.К.Толпыго, "Математические задачи", изд.3-е "Наука", 1971, задача147.) .

Итак, мы рассматриваем теперь только n m .

Если a_n b , то a_n+1=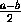 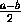<b . Таким образом, все следующие за a_m члены последовательности будут меньше b и поэтому при всех n m

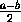
Рис.97.3. Члены последовательности a_n , определяемой условиями a₀=a , a_n+1=|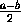| – абсциссы вершин ломаной, окрашенной в зеленый цвет. Звенья этой ломаной попеременно параллельны осям Ox , Oy , а ее вершины лежат попеременно на прямой с уравнением y=x и на графике функции y=|| .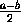

Уравнение x=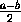 имеет единственное решение x= 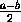. Поэтому если у последовательности {a_n} существует предел, то он равен .

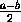Пусть a_m 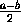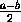. Положим a_n=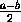+δ_n . Тогда из(eq97.2) следует, что 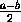+δ_n+1=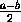- 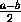, т.е.

– при переходе от n к n+1 разность a_n-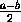=δ_n меняет знак и по абсолютной величине уменьшается вдвое. Теперь все ясно: в последовательности a_n никакое число не может встретиться дважды, поскольку каждый член ближе к 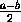, чем предыдущий. Эта последовательность не монотонна, но стремится к пределу 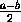(рис.3, 4).

К сожалению, некоторые читатели пишут: "Поскольку последовательность не монотонная, она не стремится к пределу". Это рассуждение, конечно, неверно. Докажем строго, пользуясь определением предела, что

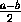
Пусть задано ε>0. Тогда если n>N , где N=N(ε)– наименьшее целое число, для которого 2^N ε>2^m |δ_m| , то |a_n-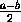|=|δ_n|=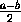< <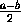ε . Тем самым(eq97.4) доказано.

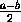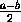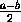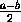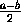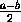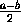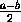Разумеется, предел равен и в том случае, когда a_m= – в этом случае все последующие члены тоже равны . Выясним, при каких значениях a возникает этот случай. Если m=0, то a= . Если m=1 и a₁== , то a= . Вообще, если a_m= , то a=a₀ получается из a_m= 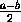после m -кратного применения формулы a_n-1=2a_n+b . Таким образом, как нетрудно проверить, значения a , при которых a_m=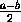 , составляют последовательность 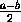, , 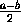, 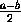... , 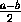, ... При этих (и только этих) значениях a последовательность получается монотонной (и с некоторого места– постоянной).

Мы не выделили отдельно случай, когда a_m=b (при этом a_m+1=0, a_m+2= 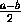, ... ),– с алгебраической точки зрения он ничем не примечателен, но соответствующие n=m и n=m+1 трапеции вырождаются в параллелограмм и в треугольник (точки B_m+1 и C_m+1 совпадают, рис.5); начиная с n=m+2, получаются настоящие трапеции, и, как всегда, a_n стремится к пределу .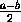

Ответ задачи отсутствует