Пусть  u³ = 1 – x,  v³ = 1 + x.  Из уравнения  u + v = p  получаем  v³ + v³ + 3uv(u + v) = p³,  откуда  2 + 3uvp = p³,  то есть 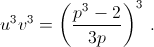    Теперь u³ и v³ находятся как корни квадратного уравнения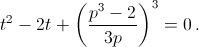  

  В итоге получаем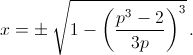  

  Поскольку 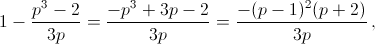    то полученный ответ имеет смысл при  p = –1  и  0 < p ≤ 2.

  Однако при наших преобразованиях могли возникнуть посторонние корни. Действительно, уравнение  u³ + v³ – p³ + 3uvp = 0  можно записать в виде  (u + v)³ – p³ – 3uv(u + v – p) = 0  ⇔  (u + v – p)(u² + v² + p² + up + pv – uv) = 0.

  Левая часть равна нулю, когда хоть одна скобка равна нулю:

    1)  u + v – p = 0,

    2)  u² + v² + p² – (up + pv – uv) = 0.

  Первое равенство – это наше исходное уравнение. Все посторонние решения связаны со вторым, и надо выяснить, когда оно выполняется. Умножив его на 2, получим:  (u + p)² + (v + p)² + (u – v)² = 0.  Это равенство выполняется только при  u = v = – p,  то есть при  x = 0,  p = – 1.

И действительно  (1 + x)^1/3 + (1 – x)^1/3 ≠ –1  при  x = 0.

При 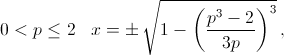    при других значениях p таких x не существует.