Задача
В остроугольном треугольнике $ABC$ отмечены точки $I$ и $O$ — центры вписанной и описанной окружностей соответственно. Прямые $AI$ и $CI$ вторично пересекают описанную окружность треугольника $ABC$ в точках $N$ и $M$. Отрезки $MN$ и $BO$ пересекаются в точке $X$. Докажите, что прямые $XI$ и $AC$ перпендикулярны.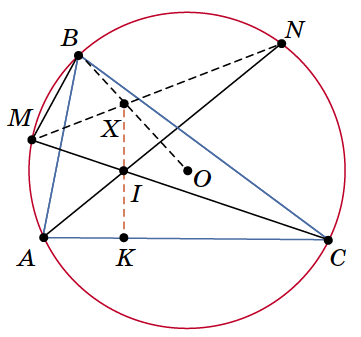
Решение
Заметим, что $M$ и $N$ — середины дуг $AB$ и $BC$ соответственно. Поэтому треугольники $MBN$ и $MIN$ равны по общей стороне и двум прилежащим углам. Значит, треугольники $MBX$ и $MIX$ равны по двум сторонам и углу между ними. Тогда
$$
\angle KIC = \angle MIX = \angle MBX =\angle MBA + \angle ABO =\ =\frac12\angle C + \frac12(180^\circ - \angle2C) = 90^\circ - \angle KCI,
$$
то есть угол $IKC$ прямой, что и требовалось.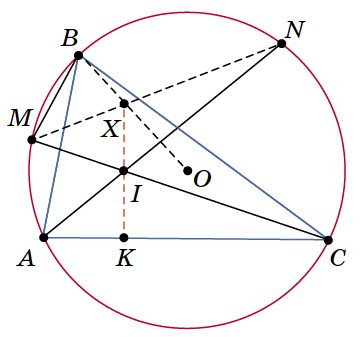
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь