Задача
Петя и Вася по очереди проводят дороги на плоскости, начинает Петя. Дорога — это горизонтальная или вертикальная прямая, по которой можно двигаться только в одну сторону (выбранную при создании дороги). Всегда ли Вася может действовать так, чтобы после любого его хода можно было проехать по правилам от любого перекрёстка дорог до любого другого, как бы ни действовал Петя?
Решение
Пусть, пока все дороги параллельны, Вася сохраняет это, следя за тем, чтобы крайние дороги были разных направлений. Когда Петя проведёт пересекающую их дорогу, Вася с одной из сторон от неё проводит дорогу противоположного направления так, чтобы возникбольшой цикл(цикл из четырёх крайних дорог, красный на рисунке).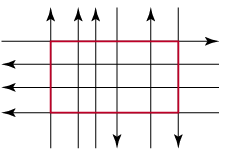
Далее Вася следит только за крайними дорогами — если они по-прежнему образуют цикл, он проводит любую не крайнюю дорогу (и большой цикл сохраняется), а если Петя испортил большой цикл, проведя крайнюю дорогу, Вася восстанавливает его, проводя рядом с Петиной новую крайнюю дорогу нужного направления. Докажем, что так Вася добьётся своей цели. Рассмотрим произвольные перекрёстки $A$ и $B$. Выедем из $A$ на большой цикл, по нему доедем до дороги, которая ведёт к перекрёстку $B$, и проедем в $B$.
Ответ
Всегда.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь