Задача
Точки $P$, $Q$ лежат внутри окружности $\omega$. Серединный перпендикуляр к отрезку $PQ$ пересекает $\omega$ в точках $A$ и $D$. Окружность с центром $D$, проходящая через $P$ и $Q$, пересекает $\omega$ в точках $B$ и $C$. Отрезок $PQ$ лежит внутри треугольника $ABC$. Докажите, что $\angle ACP = \angle BCQ$.
Решение
Решение 1:Пусть $I$ – точка пересечения отрезка $AD$ и дуги $BPQC$. Так как $DB = DC$, то $AD$ – биссектриса угла $BAC$ и по теореме о трилистнике $I$ – центр вписанной в треугольник $ABC$ окружности. Следовательно, $CI$ – биссектриса угла $ACB$. С другой стороны, так как $AD$ – серединный перпендикуляр к $PQ$, то $PI = QI$, то есть $CI$ – биссектриса угла $PCQ$. Из этих двух утверждений, очевидно, следует утверждение задачи.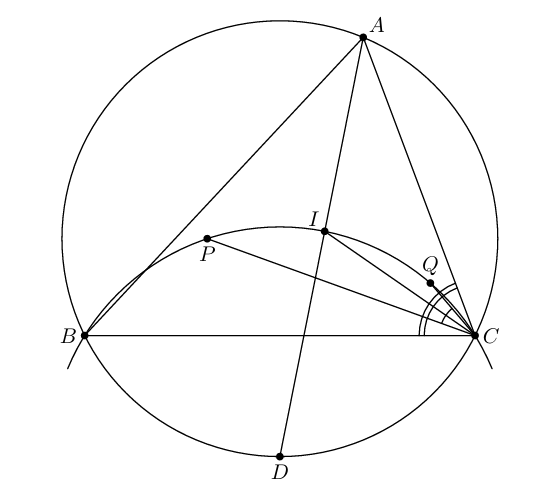
Решение 2:Обозначим $\angle ACQ = \alpha$, $\angle QCP = \beta$, $\angle PCB=\gamma$. Необходимо доказать, что $\gamma = \alpha$. Заметим, что $\alpha + \beta + \gamma = \angle ACB = \angle ADB = \angle BDP + \angle PDA$. Далее, $\angle BDP = 2 \angle BCP = 2\gamma$ как центральный и вписанный в окружность $(DPQ)$, а также $\angle PDA = \frac12 \angle PDQ = \frac12\cdot 2\angle PCQ = \beta$ как центральный и вписанный в окружность $(DPQ)$. Тогда $\alpha + \beta + \gamma = \angle BDP + \angle PDA = 2\gamma + \beta$, откуда $\gamma=\alpha$.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь