Задача
В каждой клетке таблицы $N\times N$ записано число. Назовём клетку $C$хорошей, если в какой-то из клеток, соседних с $C$ по стороне, стоит число на 1 больше, чем в $C$, а в какой-то другой из клеток, соседних с $C$ по стороне, стоит число на 3 больше, чем в $C$. Каково наибольшее возможное количество хороших клеток?
Решение
Пример расстановки для таблицы $5 \times 5$ показан на рисунке, в общем случае он строится аналогично (таблица симметрична относительно диагонали, ведущей из левого нижнего угла в правый верхний, все числа хорошие, кроме чисел на этой диагонали).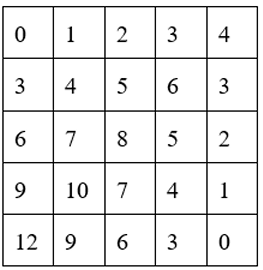
Докажем, что хороших чисел не более $N^2 - N$. Пусть их всего $X$. Соединим каждое хорошее число с двумя его соседями – с тем соседом, который на 1 больше, и с тем, который на 3 больше (соединяем отрезком). Тогда каждое хорошее число даст по два отрезка, каждый из которых будет подсчитан ровно один раз. Итого, всего будет 2$X$ отрезков. Но всего на доске пар соседних клеток ровно $2N(N −1)$, откуда 2$N(N$ – 1) ≥ 2$X$, что и требовалось.
Ответ
$N^2 - N$.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь