Задача
Высоты остроугольного треугольника $ABC$ пересекаются в точке $H$. Пусть $P$ – произвольная точка внутри (и не на сторонах) треугольника $ABC$, лежащая на описанной окружности треугольника $ABH$, и $A', B', C'$ – проекции точки $P$ на прямые $BC, CA, AB$. Докажите, что описанная окружность треугольника $A'B'C'$ проходит через середину отрезка $CP$.
Решение
Пусть $M$ – середина $CP$. Точки $A'$ и $B'$ лежат на окружности с диаметром $CP$ и центром в $M$, а вписанный в эту окружность угол $A'CB'$ острый, поэтому $\angle A'MB' = 2\angle BCA$ и $M$ лежит от прямой $A'B'$ по ту же сторону, что и $С$. Так как $P$ лежит внутри остроугольного треугольника, её проекции $A'$, $B'$, $C'$ лежат внутри сторон, тогда четырёхугольники $AB'PC'$ и $BA'PC'$ вписанные. Используя равенства вписанных углов, имеем:
180° $- \angle A'C'B' = \angle AC'B' + \angle BC'A' = \angle BPA' + \angle APB'$ = 360° $- \angle APB - \angle A'PB'$ = (180° $- \angle AHB)$ + (180° $- \angle A'PB') = \angle BCA + \angle BCA = 2\angle BCA,$
откуда $\angle A'MB' + \angle A'C'B'$ = 180°, то есть точки $A', M, B', C'$ лежат на одной окружности, что и требовалось.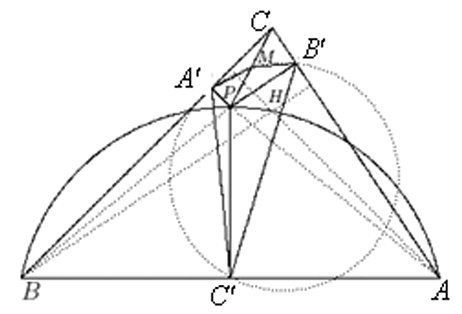
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь