Задача
Четырёхугольник $ABCD$ выпуклый, его стороны $AB$ и $CD$ параллельны. Известно, что углы $DAC$ и $ABD$ равны, а также углы $CAB$ и $DBC$ равны. Обязательно ли $ABCD$ – квадрат?
Решение
Пусть $A$, $D$, $C$, $B$ – последовательные вершины правильного шестиугольника. Тогда $ABCD$ – равнобедренная трапеция (половина правильного шестиугольника), и все упомянутые в условии углы равны $30^\circ$.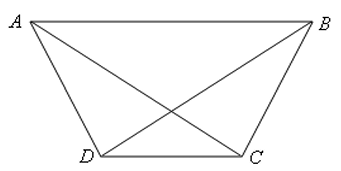
Ответ
Не обязательно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет