Задача
У Пети было 18 одинаковых по внешнему виду монет – две по 1 г, две по 2 г, две по 3 г, ..., две по 9 г. Он разложил их на подносе по кругу, как показано на рисунке. Потом поднос как-то повернули, и теперь непонятно, где какая монета. Как за два взвешивания на чашечных весах без гирь это определить?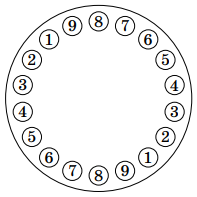
Решение
Проведём линию через центр круга (см. рис.).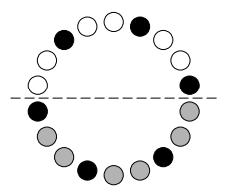 Монеты ниже линии все разные, сумма их масс 45. Чёрные монеты ниже линии — либо 1, 4 и 7 (первый случай), либо 2, 5, 8 (второй случай), либо 3, 6, 9 (третий случай). Чёрные монеты выше линии – такие же, как и ниже. Положим серые монеты на одну чашу весов, чёрные на другую, и сравним их массы:
Монеты ниже линии все разные, сумма их масс 45. Чёрные монеты ниже линии — либо 1, 4 и 7 (первый случай), либо 2, 5, 8 (второй случай), либо 3, 6, 9 (третий случай). Чёрные монеты выше линии – такие же, как и ниже. Положим серые монеты на одну чашу весов, чёрные на другую, и сравним их массы:
| Случаи | Сумма чёрных | Сумма серых | Весы покажут |
|---|---|---|---|
| Первый | $2 \cdot (1 + 4 + 7) = 24$ | $45 - 1 - 4 - 7 = 33$ | Перевес серых |
| Второй | $2 \cdot (2 + 5 + 8) = 30$ | $45 - 2 - 5 - 8 = 30$ | Равновесие |
| Третий | $2 \cdot (3 + 6 + 9) = 36$ | $45 - 3 - 6 - 9 = 27$ | Перевес чёрных |
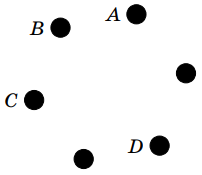 Сравним $A+C$ и $B+D$. Возможны три случая:
Сравним $A+C$ и $B+D$. Возможны три случая:
| Случаи | $A+C$ | $B+D$ | Весы покажут |
|---|---|---|---|
| $A=3$ | $3+9$ | $6+6$ | Равновесие |
| $A=6$ | $6+3$ | $9+9$ | $A+C < B+D$ |
| $A=9$ | $9+6$ | $3+3$ | $A+C > B+D$ |
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь