Задача
На одной из медиан треугольника $ABC$ нашлась такая точка $P$, что $\angle PAB=\angle PBC=\angle PCA$. Докажите, что на другой медиане найдется такая точка $Q$, что $\angle QBA=\angle QCB=\angle QAC$.
Решение
Пусть $P$ лежит на медиане из вершины $B$. Тогда $AC$ касается окружности $CPB$, а значит, и окружности $APB$, потому что медиана является их радикальной осью. С другой стороны, окружность $APB$ касается стороны $BC$, следовательно, $AC=BC$ и точка $Q$, симметричная $P$ относительно оси симметрии треугольника удовлетворяет условию.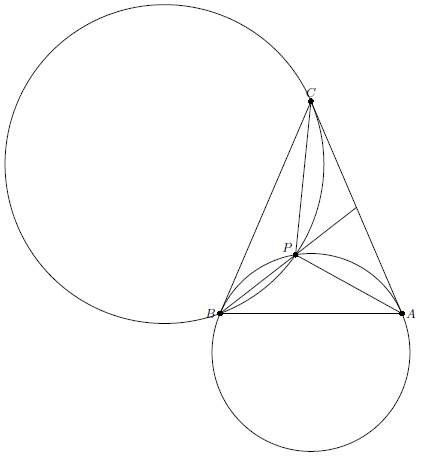
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет