Пусть $M$ – середина $AB$. Тогда $B, O, P, M$ лежат на окружности с диаметром $OB$, а $A, H, P, M$ лежат на окружности с диаметром $AH$. Отсюда $\angle PAH = \angle PMH = \angle PMO = \angle PBO$.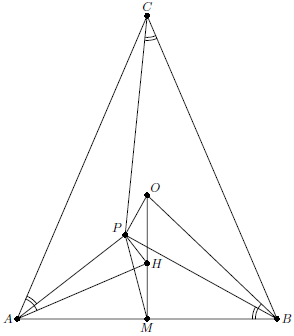Видим, что $PAH\sim PBO$, иначе говоря, $P$ – центр поворотной гомотетии, переводящей $\vec{AH}$ в $\vec{BO}$. Но из простого счета углов ($\angle OBC = \angle OCB = 90^{\circ} - \angle ABC = \angle HAB = \angle HBA$) следует, что $AHB\sim BOC$. Это значит, что поворотная гомотетия, о которой говорилось выше, переводит также $B$ в $C$. Значит, $PAB\sim PBC$, откуда $\angle PCB = \angle PBA$ и $\angle PBC = \angle PAB$. Тогда $\angle PAC = \angle BAC - \angle PAB = \angle CBA - \angle PBC = \angle PBA$, и все доказано.

Ответ задачи отсутствует