Решение 1:Так как $AP$ содержит высоту треугольника $ABI$, то $AP\perp BI$. Пусть $K$ – точка касания $AB$ со вписанной окружностью, так что $K=PI\cap AB$.Тогда $TA/PA = KA/PA = \sin \angle APK = \sin \angle ABI = \sin \frac{\angle B}{2}.$

Аналогично, $CQ\perp BI$, откуда $CQ\parallel AP$. И также $TC/QC = \sin \frac{\angle B}{2}$, откуда $TA/PA=TC/QC$.

Таким образом, $TAP\sim TCQ$. Значит, $\angle ATP = \angle CTQ$, откуда и следует, что $T$, $P$, $Q$ на одной прямой.

Решение 2:Случай $AB=BC$ очевиден. Иначе основания $F$ и $E$ высот $AF$ и $CE$ лежат на биссектрисе $BI$ по разные стороны от $AC$, прямые $AP$ и $CQ$ параллельны и $\angle PAT = \angle FAT = \angle ECT = \angle QCT$.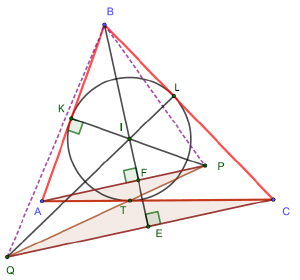 Задача будет решена, если мы докажем подобие треугольников $TAP$ и $TCQ$ (тогда равные углы $CTQ$ и $ATP$ вертикальны и точки $P$, $Q$, $T$ лежат на одной прямой). Для этого достаточно проверить, что $AT/AP=CT/CQ$. Пусть $K$ и $L$ – точки касания окружности со сторонами $AB$ и $BC$ соответственно. Тогда $AT=AK$ и $CT=CL$, и осталось доказать равенство $AK/AP=CL/CQ$. Оно следует из подобия треугольников $APK$ и $CQL$: они прямоугольные, а поскольку $BI$ – биссектриса угла $B$, углы $BAP$ и $BCQ$ равны.

Ответ задачи отсутствует