Задача
Город $N$ представляет собой клетчатый квадрат $9\times9$. За $10$ минут Таня может перейти из любой клетки в соседнюю по стороне. Ваня может открыть в любых двух клетках по станции метро – после этого можно будет перемещаться из одной такой клетки в другую за $10$ минут. Отметьте две клетки, в которых Ване нужно открыть метро, чтобы Таня могла добраться из любой клетки города в любую другую за $2$ часа.
Решение
Откроем метро в самой верхней и самой нижней клетках центрального столбца (отмечены на рисунке фиолетовым). Докажем, что теперь можно добраться из любой клетки A в любую клетку B не более чем за два часа.
Два часа – это 120 минут, то есть, после открытия станций из любой клетки в любую другую нужно добраться не более чем за 12 ходов от клетки к клетке.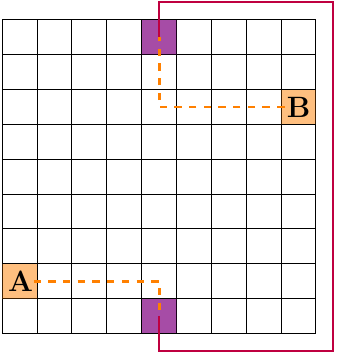 Составим маршрут из трёх частей (пример маршрута показан на рисунке):
Составим маршрут из трёх частей (пример маршрута показан на рисунке):
-
от точки А по горизонтали пройти до центрального столбца – не более 4 ходов;
-
по центральному столбцу переместиться из горизонтали, содержащей точку A, в горизонталь точки B;
-
от центрального столбца по горизонтали пройти до точки B – не более 4 ходов.
Посмотрим, сколько ходов может занять второй этап. В центральном столбце 9 клеток, при этом из верхней клетки можно перейти в нижнюю – то есть можно представить центральный столбец как кольцо из 9 клеток. Между любыми двумя клетками этого кольца есть два пути (в одну или в другую сторону), причём кратчайший путь содержит не более 4 ходов. Значит, все три этапа в сумме займут не более 4+4+4=12 ходов, как и требовалось.
Ответ
Например, подойдут верхняя и нижняя клетки центрального столбца.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь