Раскрасим доску и монеты на ней в шахматном порядке (угловые клетки чёрные). Отметим, что обе фальшивые монеты одного цвета. а) Способ 1. Положим на весы 16 монет, лежащих на краю доски: на одну чашку – 8 чёрных, на другую – 8 белых. Возможны три случая.

1. Весы в равновесии. Так как фальшивые монеты могли быть на только на одной чаше, их нет среди взвешиваемых монет, то есть все 16 взвешиваемых монет настоящие.
2. Перевесила «чёрная» чашка. Тогда одна фальшивая монета – на «белой» чашке. Следовательно, все 13 чёрных монет настоящие.
3. Перевесила «белая» чашка. Тогда одна фальшивая монета – на «чёрной» чашке. Поэтому центральная монета настоящая. И все 12 белых монет тоже. Обобщение. Отложим любую чёрную монету A и всех её соседей по диагонали. Из оставшихся чёрных монет положим на одну чашу не менее 7, а на другую – столько же белых. При равновесии все монеты на весах настоящие (их не меньше 14). Если перевесят чёрные, то все чёрные монеты настоящие, а если белые, то все белые и A. Способ 2. Положим на чаши 4 чёрные монеты, соседние с центральной, левые – на левую, правые – на правую. При равновесии все чёрные монеты настоящие (так как две фальшивые чёрные монеты не могут быть ни на разных чашах, ни обе вне чаш). Если какая-то чаша перевесит, то настоящие – две монеты на этой чаше и все белые монеты.

б) Способ 1. Взвесим чёрные монеты против белых на рисунке слева.

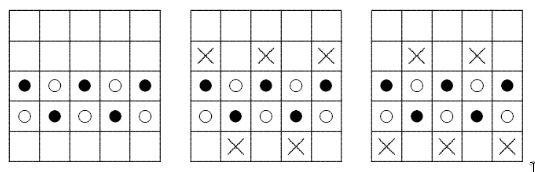В случае равновесия 15 монет в нижних трёх строках настоящие. Если чёрные монеты тяжелее, не взвешиваемая фальшивая монета может находиться только в квадратах, отмеченных крестиками на рис. в центре. Следовательно, мы нашли 25 – 5 – 5 = 15 настоящих монет. Если белые монеты тяжелее, ситуация показана на рисунке справа с тем же результатом.

Способ 2. Взвесим чёрные монеты против белых на левом рисунке. 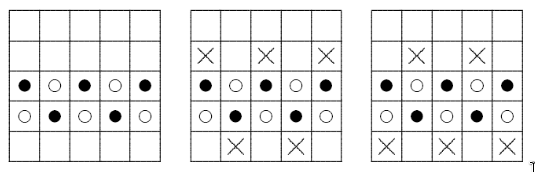В случае равновесия все 16 взвешиваемых монет настоящие. Если чёрные монеты тяжелее, не взвешиваемая фальшивая монета может находиться только в двух квадратах, отмеченных крестиками на центральном рисунке. Таким образом, найдены 25 – 8 – 2 = 15 настоящих монет. Если белые монеты тяжелее, получим тот же результат (правый рисунок.

Способ 3. Из пятой строки две белые монеты положим на левую чашку, две чёрные – на правую, а одну монету отложим. Остальные белые – на правую, чёрные – на левую чашку. При равновесии все монеты из первых трёх строк настоящие. Если какая-то чашка перевесит, то настоящие – все 12 монет на ней и все монеты из пятой строки (итого 15 монет).

в) Априори любая из 25 монет подозрительна (может быть фальшивой). Взвешивание может иметь 3 исхода, поэтому хотя бы при одном из них подозрительными останутся не меньше 9 монет, то есть будет найдено не более 25 – 9 = 16 настоящих монет.

а) можно; б) можно; в) нельзя.