Подходит, например, любой треугольник, где AB = AC = 2. Докажем, что трёх равных сторон быть не может.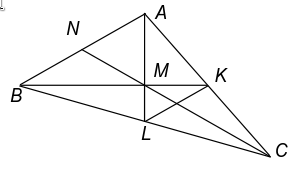

Способ 1. Предположим, что хотя бы три стороны четырёхугольника ANMK равны 1. Возможны всего два принципиально различных случая.

1. AN = NM = MK = 1. Тогда NB = 1, MB = 2, значит, MN + NB = MB.
2. KA = AN = NM = 1. Тогда AC = 2, NC = 3, значит, NA + AC = NC. В обоих случаях получено противоречие с неравенством треугольника.

Способ 2. Если более двух сторон четырёхугольника равны 1, то либо AK = NA, либо KM = MN. В первом случае треугольник ABC равнобедренный. Во втором случае BK = CN = 3, так что и в этом случае треугольник ABC равнобедренный. Отсюда следует, что AK = KM = MN = NA, то есть AKMN – ромб. Противоречие, так как прямые AK и NM не параллельны.

Способ 3. Пусть L – середина стороны BC. Если NM = NA = NB, то треугольник AMB прямоугольный. Треугольник LMK подобен треугольнику AMB с коэффициентом 0,5, поэтому MK < LK = NA. Далее, AM > LM, поэтому у треугольника AMK гипотенуза больше, чем у треугольника LMK, то есть AK > LK = NA. Таким образом в четырёхугольнике ANMK нет трёх равных друг другу сторон.

Случай, когда KM=KA аналогичен, а если KM ≠ KA и NM ≠ NA, то среди отрезков NM, NA, KM, KA также нет трёх равных друг другу.

2 стороны.