Возьмем квадрат $ABCD$ и заменим стороны $AB$, $AD$ равными дугами, направленными наружу, а стороны $BC$, $CD$ такими же дугами, направленными внутрь. Получим фигуру, ограниченную четырьмя дугами, которой, очевидно, можно замостить плоскость. Также можно замостить плоскость полоской из $k$ таких фигур, которая ограничена $2k+2$ дугами. Кроме того, можно выбрать радиусы дуг так, чтобы дуги $AB$ и $AD$ составили одну полуокружность.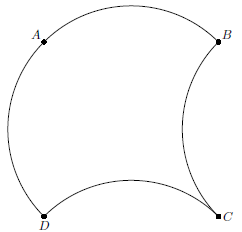 Тогда получится фигура, ограниченная тремя дугами. Составив полоску из $k$ таких фигур, получим фигуру, ограниченную $2k+1$ дугой.

Если $n=2$, то фигура является полумесяцем, у которого внешняя дуга длиннее внутренней. Поэтому на внешней дуге найдется точка, в которой сходятся два других полумесяца. Очевидно, что угол, образованный их внешними дугами, замостить невозможно.

$n>2$.