Задача
Внутри параллелограмма $ABCD$ взята такая точка $P$, что ∠$PDA$ = ∠$PBA$. Пусть Ω – вневписанная окружность треугольника $PAB$, лежащая против вершины $A$, а ω – вписанная окружность треугольника $PCD$. Докажите, что одна из общих касательных к Ω и ω параллельна $AD$.
Решение
Перенеся треугольник $PAB$ на вектор $\overrightarrow{AD}$, получим треугольник $QDC$. Окружность Ω также сдвинется параллельно $AD$ и перейдёт во вневписанную окружность Ω' треугольника
с центром $J$, поэтому достаточно доказать, что одна из общих касательных к Ω' и ω параллельна $AD$.
По условию ∠$QPD$ = ∠$PDA$ = ∠$PBA$ = ∠$QCD$, значит, точки $C, P, D$ и $Q$ лежат на одной окружности. По известным формулам углов между биссектрисами
∠$CID$ + ∠$CJD$ = (0,5∠$CPD$ + 90°) + (90° – 0,5∠$CQD$) = 180°, то есть точки $C, I, D$ и $J$ лежат на одной окружности. Следовательно, угол между $CD$ и $IJ$ равен
∠$CDJ$ + ∠$ICD$ = 0,5∠$CDQ$ + 0,5∠$PCD$, а это и есть половина угла между хордами $CD$ и $PQ$.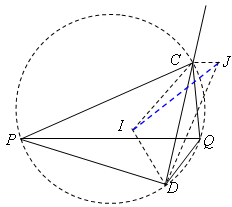
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь