Задача
Внутри остроугольного неравнобедренного треугольника $ABC$ отмечена точка $T$, такая что $\angle ATB = \angle BTC = 120^\circ$. Окружность с центром $E$ проходит через середины сторон треугольника $ABC$. Оказалось, что точки $B,T,E$ лежат на одной прямой. Найдите угол $ABC$.
Решение
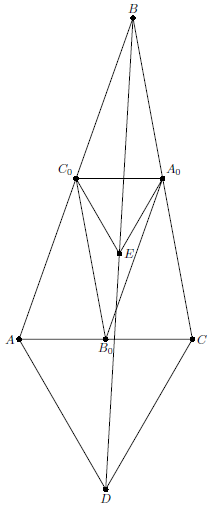
Пусть $A_0$, $B_0$, $C_0$ – середины сторон $BC$, $CA$, $AB$ соответственно, $D$ – вершина правильного треугольника $ABD$, построенного во внешнюю сторону. Известно, что точка $T$ лежит на отрезке $BD$. При гомотетии с центром $B$ и коэффициентом $1/2$ прямая $B_0D$ переходит в серединный перпендикуляр к отрезку $A_0C_0$, следовательно, $E$ – середина $BD$ и $\angle C_0EA_0=60^{\circ}$. Соответственно, $\angle ABC=\angle A_0B_0C_0=30^{\circ}$.
Ответ
$30^{\circ}$.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь