Задача
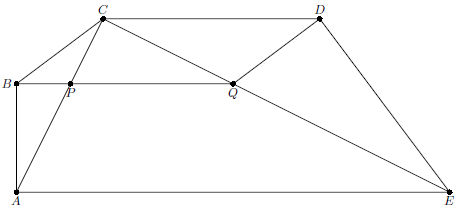
В выпуклом пятиугольнике $ABCDE$ равны углы $CAB$, $BCA$, $ECD$, $DEC$ и $AEC$. Докажите, что середина $BD$ лежит на $CE$.
Решение
Из условия следует, что $CD\parallel AE$. Пусть прямая, проходящая через $B$ и параллельная $AE$, пересекает $AC$ и $CE$ в точках $P$ и $Q$ соответственно. Тогда точки $P$ и $Q$ делят в одинаковом отношении основания $CA$ и $CE$ подобных равнобедренных треугольников $ABC$ и $CDE$. Поэтому $\angle CBQ=\angle CDQ$, $BCDQ$ – параллелограмм и середины отрезков $BD$ и $CQ$ совпадают.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет