Задача
Есть набор монет радиусами $1, 2, 3,\ldots, 10$ см. Можно положить две из них на стол так, чтобы они касались друг друга, и добавлять монеты по одной так, чтобы очередная касалась хотя бы двух уже лежащих. Новую монету нельзя класть на старую. Можно ли положить несколько монет так, чтобы центры каких-то трёх монет оказались на одной прямой?
Решение
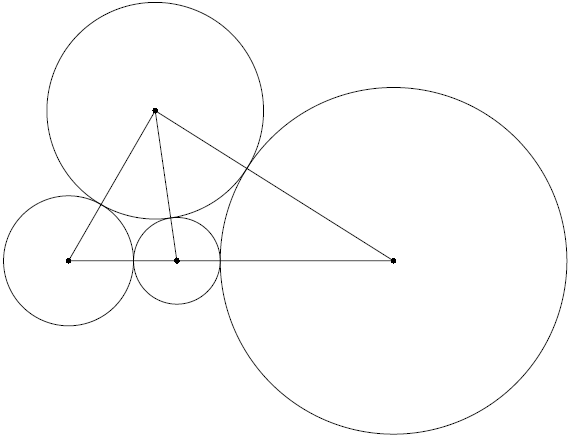
Будем искать конструкцию с четырьмя монетами (очевидно, трех монет недостаточно). Пусть монеты с радиусами $a$, $b$, $x$, $y$ расположены так, что любые две из них, кроме монет с радиусами $x$ и $y$ касаются. Обозначим через $O_r$ центр окружности с радиусом $r$. Применяя теорему косинусов к треугольнику $O_aO_bO_x$, получаем $\cos\angle O_bO_aO_x=((a+b)^2+(a+x)^2-(b+x)^2)/2(a+b)(a+x)$. Аналогично, $\cos\angle O_bO_aO_y=((a+b)^2+(a+y)^2-(b+y)^2)/2(a+b)(a+y)$. Чтобы точки $O_a$, $O_x$ и $O_y$ лежали на одной прямой, необходимо и достаточно, чтобы сумма этих выражений равнялась нулю, что эквивалентно равенству $(b-a)(ax+ay+2xy)=a(a+ b)(2a+x+y)$. Непосредственная проверка показывает, что оно выполнено при $a=2$, $b=5$, $x=3$, $y=8$ (см.рис., косинусы равны $\frac17$ и $-\frac17$).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь