Задача
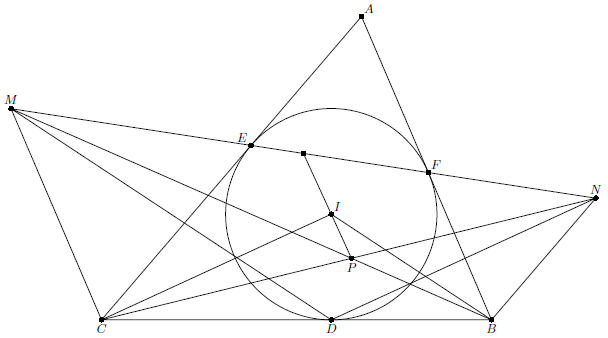
В треугольник $ABC$ вписана окружность с центром $I$, касающаяся сторон $CA$, $AB$ в точках $E$, $F$ соответственно. Точки $M$, $N$ на прямой $EF$ таковы, что $CM=CE$ и $BN=BF$. Прямые $BM$ и $CN$ пересекаются в точке $P$. Докажите, что прямая $PI$ делит пополам отрезок $MN$.
Решение
Докажем, что прямые $BM$ и $CN$ делят отрезки $IN$ и $IM$ соответственно в одном и том же отношении (внешним или внутренним образом). Тогда, применив к треугольнику $IMN$ теорему Чевы, получим утверждение задачи.
Первое отношение равно $S_{BIM}:S_{BMN}$, второе – $S_{CIN}:S_{CMN}$.
Заметим, что $AEF$, $BFN$ и $CEM$ – подобные равнобедренные треугольники. Следовательно, $$S_{BMN}:S_{CMN}=d(B, MN):d(C, MN)=BF:CE=BD:DC,$$ где $D$ – точка касания вписанной окружности со стороной $BC$.
Из подобия треугольников $AEF$, $BFN$ и $CEM$ получаем также, что $AB\parallel CM$ и $AC\parallel BN$. Поскольку $BD=BN$ и $CD=CM$, отсюда следует, что $DM\parallel BI$ и $DN\parallel CI$. Поэтому $S_{BIM}=S_{BID}$, $S_{CIN}=S_{CID}$ и $S_{BIM}:S_{CIN}=BD:DC$, ч.т.д.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь