Задача
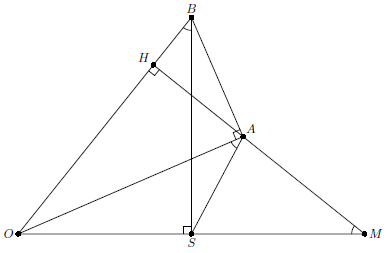
Внутри прямого угла с вершиной $O$ расположен треугольник $OAB$ с прямым углом $A$. Высота треугольника $OAB$, опущенная на гипотенузу, продолжена за точку $A$ до пересечения со стороной угла $O$ в точке $M$. Расстояния от точек $M$ и $B$ до второй стороны угла $O$ равны $2$ и $1$ соответственно. Найдите $OA$.
Решение
Решение 1:Пусть $AH$ – высота треугольника. Тогда четырехугольник $BHSM$ – вписанный, следовательно, $OH\cdot OB=OS\cdot OM=2$. Но $OH\cdot OB=OA^2$ по свойству прямоугольного треугольника.
Решение 2:
Пусть $S$ – проекция $B$ на $OM$. Тогда четырехугольник $ABOS$ – вписанный и, значит, $\angle OAS=\angle OBS=90^{\circ}-\angle BOM=\angle OMA$, т.е. треугольники $AOS$ и $MOA$ подобны. Следовательно, $OA^2=OS\cdot OM=1\cdot 2$.
Ответ
$\sqrt{2}$.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь