Задача
На клетчатой бумаге нарисовали треугольник, один из углов которого равен $45^{\circ}$ (см.рис.). Найдите значения остальных углов.
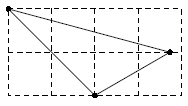
Решение
Первое решение.
Введем обозначения, как на рисунке ниже.
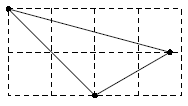 Так как $\angle A < \angle OAB = 45^{\circ} = \angle OBA < \angle B$, то $\angle C = 45^{\circ}$. Поскольку $OA=OB$ и $\angle AOB = 90^{\circ} = 2\angle ACB$, точка $O$ является центром описанной окружности треугольника $ABC$ и $OC=OB$. Но $C$ лежит на серединном перпендикуляре к отрезку $BO$, значит, $OC=BC$, треугольник $OBC$ равносторонний и $\angle BOC = 60^{\circ}$. Поэтому $\angle A=30^\circ$, $\angle B=105^{\circ}$.
Второе решение. Пусть $M$ – середина $AB$. Так как $\angle CMB=45^{\circ}$, треугольники $ABC$ и $CBM$ подобны. Поэтому $AB/BC=\sqrt{2}$, и по теореме синусов $\angle A=30^\circ$.
Так как $\angle A < \angle OAB = 45^{\circ} = \angle OBA < \angle B$, то $\angle C = 45^{\circ}$. Поскольку $OA=OB$ и $\angle AOB = 90^{\circ} = 2\angle ACB$, точка $O$ является центром описанной окружности треугольника $ABC$ и $OC=OB$. Но $C$ лежит на серединном перпендикуляре к отрезку $BO$, значит, $OC=BC$, треугольник $OBC$ равносторонний и $\angle BOC = 60^{\circ}$. Поэтому $\angle A=30^\circ$, $\angle B=105^{\circ}$.
Второе решение. Пусть $M$ – середина $AB$. Так как $\angle CMB=45^{\circ}$, треугольники $ABC$ и $CBM$ подобны. Поэтому $AB/BC=\sqrt{2}$, и по теореме синусов $\angle A=30^\circ$.
Ответ
$30^\circ$ и $105^{\circ}$.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь