Задача
Никита нарисовал и закрасил выпуклый пятиугольник с периметром $20$ и
площадью $21$. Таня закрасила все точки, находящиеся на расстоянии не более $1$ от закрашенных Никитой (см. рис.).
На сколько увеличилась закрашенная площадь? Ответ округлите до сотых.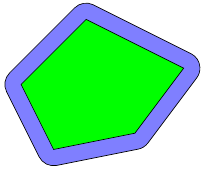
Решение
Разобьем добавленную Таней площадь на пять прямоугольников ширины $1$, у каждого из которых одна из сторон совпадает со стороной исходного пятиугольника, и на сектора кругов радиуса $1$ с вершинами в вершинах пятиугольника (см. рис).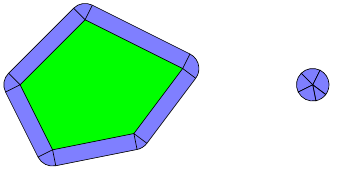 Добавленная площадь равна сумме площадей прямоугольников и площадей секторов. Сумма площадей прямоугольников равна произведению ширины (равной $1$) на сумму длин сторон пятиугольника: $1\cdot 20$.
Сектора же складываются в один полный круг,
площадь которого равна $\pi\cdot 1^2$.
То есть добавленная площадь составляет $20 + \pi \approx 23{,}14$.
Добавленная площадь равна сумме площадей прямоугольников и площадей секторов. Сумма площадей прямоугольников равна произведению ширины (равной $1$) на сумму длин сторон пятиугольника: $1\cdot 20$.
Сектора же складываются в один полный круг,
площадь которого равна $\pi\cdot 1^2$.
То есть добавленная площадь составляет $20 + \pi \approx 23{,}14$.
Ответ
$23{,}14$.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь