Решение 1:   Построим равносторонний треугольник $BCL$ (см.рисунок; точки $A$ и $L$ находятся по одну сторону от прямой $BC$).

  Точки $A, C$ и $L$ лежат на окружности радиуса $BA$ с центром в точке $B$. Поскольку $K$ лежит внутри треугольника $ABC, AC > BC$.  Значит,  ∠ABC > 60°,  откуда $L$ и $B$ лежат по разные стороны от $AC$ и $L$ лежит на меньшей дуге $AC$. Поэтому вписанный угол $CAL$ равен половине центрального угла $CBL$, то есть 30°.

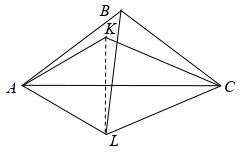
  Очевидно, точка $K$, удовлетворяющая условиям задачи, единственна, следовательно, она совпадает с точкой, симметричной $L$ относительно стороны $AC$. Значит, треугольник $AKL$ равносторонний, точка $K$, как и точка $B$, лежит на серединном перпендикуляре к отрезку $AL$, откуда  $\angle AKB=\angle LKB=180^{\circ} - \frac{1}{2} \angle AKL=150^{\circ}$.

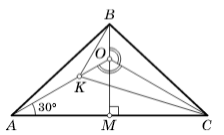
Решение 2:   Пусть высота $BM$ треугольника $ABC$ пересекается с прямой $AK$ в точке $O$ (см.рисунок).

  Тогда  $\angle COM=\angle AOM=60^{\circ}$.  Значит,  ∠AOC = 120°  и  ∠COB = 120°.  Следовательно, треугольники $BOC$ и $KOC$ равны по двум сторонам и углу, лежащей против большей из них (так называемый четвёртый признак равенства треугольников). Поэтому  $OB = OK$,  то есть треугольник $BOK$ равнобедренный с углом 120° при вершине $O$. Поэтому  ∠OKB = 30°,  а  ∠AKB = 150°.

Решение 3:   Построим на $AC$ равносторонний треугольник $ACL$ так, чтобы точки $L$ и $B$ лежали с одной стороны от $AC$ (см. рис).

  Проведём в треугольнике $ABC$ высоту $BM$, она же серединный перпендикуляр к стороне $AC$. Точка $L$ также лежит на прямой $BM$. Кроме этого, проведём в треугольнике $ALC$ высоту $AN$. Так как $AN$ – биссектриса угла $LAC$, точка K лежит на этой прямой, причём с той же стороны от $BM$, что и $A$, так как из-за  $CK = CB$  она не может лежать внутри треугольника $BMC$; таким образом, $K$ лежит на отрезке $AN$.

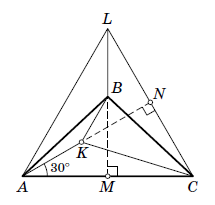
  Заметим, что прямоугольные треугольники $BMC$ и $KNC$ равны по катету и гипотенузе (так как  $MC$ = ^AC/₂ = ^LC/₂ = $NC, BC = KC$).  Отсюда следует, во-первых, что  $BM = KN$,  во-вторых, что $B$ лежит на отрезке $LM$ (так как  $BM = KN < AN = LM$),  и, наконец, что  $LB = LM - BM =AN - KN = AK$.

  Теперь рассмотрим четырёхугольник $ALBK$. В нем  ∠LAK = ∠ALB = 30°  и  $AK = LB$,  то есть это равнобокая трапеция. Отсюда следует, что  ∠AKB = 180° – ∠KAL = 150°.

Решение 4:   Пусть  ∠B = 2β.  По теореме синусов  $2BC \sin \beta = AC = KC\dfrac{\sin\angle AKC}{\sin 30^\circ} = 2BC \sin\angle AKC$,  и поскольку  ∠AKC > 2β > β,  то  ∠AKC = 180° – β.  Значит,  ∠ACK = β – 30°,

∠KCB = ∠C – ∠ACK = (90° – β) – (β – 30°) = 120° – 2β,  ∠BKC = ½ (180° – ∠KCB) = 30° + β,  ∠AKB = 360° – ∠BKC – ∠AKC = 360° – (30° + β) – (180° – β) = 150°.

150 °.