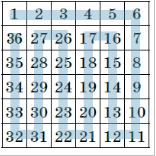
Пронумеруем столбцы и строки от 1 до $n$ соответственно слева направо и сверху вниз, а также раскрасим доску в шахматном порядке так, чтобы угловая клетка в первом столбце и первой строке была чёрной.   Пусть $n$ чётно. Заполним таблицу числами от 1 до $n^2$ так: ставим их друг за другом, начиная от 1, сначала в первой строке слева направо, а потом – вдоль столбцов: вниз по последнему столбцу, вверх по предпоследнему, и т.д. (получается что-то похожее на змейку). В итоге число $n^2$ окажется прямо под 1, см. пример для  $n$ = 6  на рисунке.

  Заменим теперь числа на их остатки по модулю $n$ (см. рисунок).   Нетрудно доказать, что они расставлены следующим образом: для нечётного столбца последнее (нижнее) число совпадает с первым числом следующего чётного столбца и вторым числом следующего нечётного.

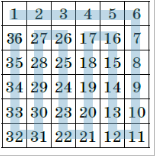
  Значит, каждый столбец начинается с остатка $i$, равного своему номеру, кроме n-го, который начинается с нуля, причём в чётных столбцах остатки идут по возрастанию c $i$ до  $n - 1$,  а потом с нуля до  $i-1$,  а в нечётных – по убыванию с i до 0, а потом с  n - 1$ до  i + 1$.

  Докажем, что в каждой строке все остатки различны. Пусть в какой-то строке совпали два остатка. Они не могут находиться в столбцах одной чётности – такие столбцы получаются друг из друга циклическим сдвигом. Значит, один остаток находится в чётном столбце, а второй – в нечётном. Но тогда эти два остатка стоят на клетках разного цвета и не могут совпадать. Противоречие.   Предположим, что удалось заполнить таблицу при нечётном $n$. К противоречию можно прийти по-разному.   Первый способ. Заметим, что в нашей раскраске чёрными окажутся те клетки, сумма номеров строки и столбца которых чётна, а белыми – остальные. В нашей змейке чисел от 1 до $n^2$ цвета клеток чередуются, поэтому числа одной чётности находятся в чёрных клетках, а другой чётности – в белых.

  Рассмотрим клетки таблицы, в которых стоят числа, дающие остаток $k$ при делении на $n$. Сумма их номеров строк и столбцов по условию равна  $(1 + 2 + 3 + ... + n) + (1 + 2 + 3 + ... + n)$,  так как каждая строка и каждый столбец участвуют по одному разу; в частности, эта сумма чётна. Но у каждой белой клетки сумма "координат" нечётна, а у каждой чёрной – чётна, следовательно, число белых клеток среди рассмотренных чётно.

  Взяв  $k$ = 1  и  $k$ = 2,  получаем, что среди чисел с остатком 1 чётное количество находится на белых клетках, и среди чисел с остатком 2 – тоже. Но для каждого числа с остатком 1 следующее за ним число имеет остаток 2 и стоит на клетке противоположного цвета. Значит, на чёрных клетках стоит чётное количество чисел с остатком 2 и всего чисел с остатком 2 чётно. Противоречие с нечётностью $n$.

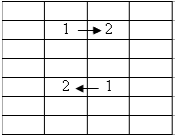
  Второй способ Заменим числа на их остатки от деления на $n$ и проведём стрелку из каждой клетки с единицей в соседнюю клетку с двойкой. У нас имеется $n$ стрелок, соединяющих единицы и двойки. У некоторых стрелок могут быть парные – стрелки противоположного направления, занимающие те же два ряда (см. рисунок). Но число стрелок нечётно, поэтому найдётся стрелка без пары.

  Пусть, например, такая стрелка горизонтальна и ведёт из i-го столбца в (i+1)-й (см.рисунок).   В (i+1)-м столбце тоже есть единица. Поскольку у первой стрелки нет пары, вторая стрелка может вести только в (i+2)-й столбец (двойка в (i+1)-м столбце уже занята). В (i+2)-м столбце тоже есть единица, и стрелка из неё может вести только в (i+3)-й столбец (двойки в (i+1)-м и (i+2)-м столбцах уже заняты). Продолжая, дойдём до единицы в n-м столбце, откуда стрелке идти уже некуда. Противоречие.

При всех чётных $n$.