Задача
К плоскости приклеены два непересекающихся деревянных круга одинакового размера – серый и чёрный. Дан деревянный треугольник, одна сторона которого серая, а другая – чёрная. Его передвигают так, чтобы круги были снаружи треугольника, причём серая сторона касалась серого круга, а чёрная – чёрного (касание происходит не в вершинах). Докажите, что прямая, содержащая биссектрису угла между серой и чёрной сторонами, всегда проходит через одну и ту же точку плоскости.
Решение
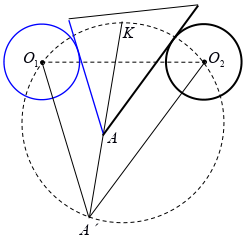
Точки биссектрисы угла $A$ между серой и чёрной сторонами деревянного треугольника равноудалены от этих сторон (серый цвет изображаем синим).Проведём через центры $O_{1}$ и $O_{2}$ серого и чёрного кругов прямые, параллельные этим сторонам. Пусть они пересекаются в точке $A'$. Поскольку угол $O_{1}A'O_{2}$, равный углу $A$, постоянен, описанная окружность Ω треугольника $O_{1}A'O_{2}$ не зависит от положения исходного треугольника. Так как радиусы серой и черной окружностей равны, точки прямой, содержащей указанную биссектрису , равноудалены от прямых $O_{1}A'$ и $O_{2}A'$, то есть эта прямая содержит биссектрису угла $O_{1}A'O_{2}$. Следовательно, она проходит через середину $K$ дуги $O_{1}O_{2}$ окружности Ω.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь