Задача
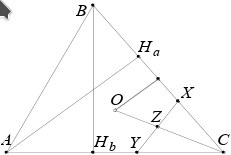
В остроугольном неравнобедренном треугольнике $ABC$ с центром описанной окружности $O$ проведены высоты $AH_a$ и $BH_b$. Точки $X$ и $Y$ симметричны точкам $H_a$ и $H_b$ относительно середин сторон $BC$ и $CA$ соответственно. Докажите, что прямая $CO$ делит отрезок $XY$ пополам.
Решение
Заметим, что $CX : CY = BH_a : AH_b = \cos\angle B : \cos\angle A$.
Кроме того, $\sin\angle OCX = \cos\angle A, \sin\angle OCY = \cos\angle B$. Отсюда $ZX : ZY = S_{CZX} : S_{CZY} = CX \sin\angle OCX : CY \sin\angle OCY = 1 : 1$, что и требовалось.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет