Задача
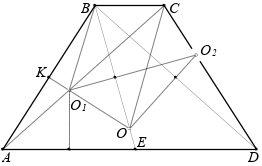
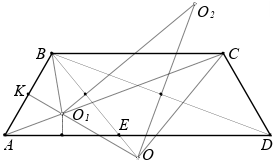
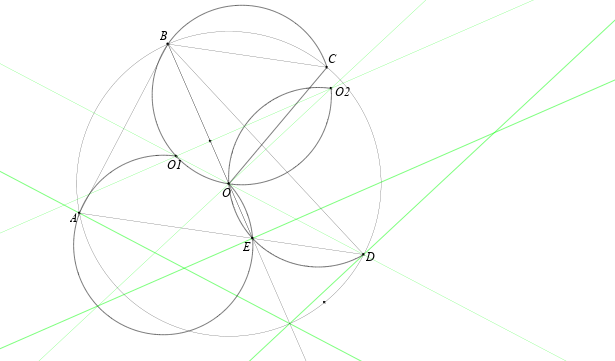
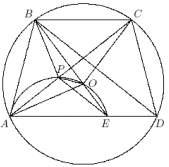
Равнобокая трапеция $ABCD$ с основаниями $AD$ и $BC$ вписана в окружность с центром $O$. Прямая $BO$ пересекает отрезок $AD$ в точке $E$. Пусть $O_1$ и $O_2$ — центры описанных окружностей треугольников $ABE$ и $DBE$ соответственно. Докажите, что точки $O_1, O_2, O, C$ лежат на одной окружности.
Решение
Нетрудно понять, что $AD$ – большее основание, треугольник $AEB$ остроугольный, и точки $B, C$ и $O_2$ лежат по одну сторону от прямой $OO_1$. Прямые $OO_1, O_1O_2$ и $OO_2$ – серединные перпендикуляры к $AB, BE$ и $BD$ соответственно. Пусть $K$ – середина $AB$.
Первый способ. Так как $\angle BO_1O_2 = \angle BAD = \angle BOO_2$ (половина центрального угла равна вписанному для треугольников $BAE$ и $BAD$), то, четырёхугольник $OO_1BO_2$ вписанный. Поскольку $\angle KO_1B = \angle AEB = \angle CBE = \angle CBO = \angle BCO$, то четырёхугольник $OO_1BC$ вписанный.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь