Решение 1:Поскольку в прямоугольном треугольнике $CLB$ медиана, проведенная из прямого угла, равна половине гипотенузы, достаточно доказать, что $M$ – середина $LB$. Первый способ. Отметим на отрезке $AK$ точку $F$ так, что  $AF = AL$.  Тогда  $FL \parallel KC$  и  $FK = LC = KB$.  Значит, $KM$ – средняя линия треугольника $LFB$, и  $LM = MB$.

Второй способ. Проведём через точку $L$ прямую, параллельную $AB$, до пересечения с $CK$ в точке $G$. Так как треугольник $CAK$ равнобедренный, то и $CLG$ – тоже. Поэтому  $LG = LC = BK$  и $LGBK$ – параллелограмм. Следовательно, $M$ – середина $LB$.Третий способ. Поместим в точки $C, A$ и $B$ массы  $x = AL$,  $y = LC$  и  $x + y$  соответственно. Тогда $L$ – центр масс точек $A$ и $C$, а $K$ – точек $A$ и $B$. Поэтому общий центр масс лежит на пересечении отрезков $BL$ и $CK$, то есть в точке $M$. Группируя точки $A$ и $С$, получим точку $L$ с массой  $x + y$.  Поскольку у $L$ и $B$ равные массы, то $М$ – середина $LB$. Четвертый способ. Проведём через точку $B$ прямую $l$, параллельную $AC$, и продлим $CK$ до пересечения с $l$ в точке $P$. Треугольники $NBK$ и $CAK$, очевидно, подобны, поэтому  $BP = BK = LC$,  то есть $LCBP$ – прямоугольник, а точка пересечения его диагоналей. Следовательно, $MC = ML$.

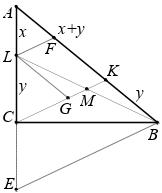Решение 2:Проведём через точку $B$ прямую, параллельную $CK$, до пересечения с прямой $AC$ в точке $E$. Так как треугольник $ACK$ равнобедренный, то и $AEB$ – тоже. Поэтому  $EC = BK = LC$.  Таким образом, $BC$ – высота и медиана треугольника $ELB$, значит, он равнобедренный. Подобный ему треугольник $CLM$ тоже равнобедренный.

Ответ задачи отсутствует