Задача
Дана окружность $\omega$ и ее хорда $BC$. Точка $A$ движется по большей из дуг $BC$. Пусть $H$ – ортоцентр треугольника $ABC$, $D$, $E$ – такие точки на сторонах $AB$, $AC$, что $H$ – середина отрезка $DE$, $O_A$ – центр описанной окружности треугольника $ADE$. Докажите, что все точки $O_A$ лежат на одной окружности.
Решение
Обозначим постоянный угол $90^{\circ}-\angle BAC$ через $\alpha$. Пусть $P$, $Q$ – середины $AD$, $AE$, а $R$, $S$ – такие точки на прямой $BC$, что $PR\perp AB$, $SQ\perp AC$ (см. рис.). Покажем, что точки $R$, $S$ не зависят от $A$.
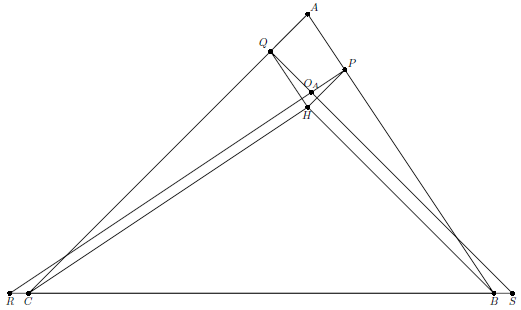Заметим, что $HQ\parallel AB$, т.е. $\angle CHQ=90^{\circ}$ и $\angle CQH=\angle CAB$. Кроме того, $H$ движется по окружности, симметричной $\omega$ относительно $BC$. Поскольку $Q$ – образ $H$ при поворотной гомотетии с центром $C$, углом поворота $\alpha$ и коэффициентом $1/\cos\alpha$, $Q$ также движется по некоторой окружности, обозначим ее $\omega_C$.
Пусть $O$ – центр $\omega$. Так как $\angle OCB=\alpha$, центр $\omega_C$ лежит на $BC$. Поскольку $\angle CQS=90^{\circ}$, $S$ – диаметрально противоположная $C$ точка окружности $\omega_C$. Следовательно, $S$ не зависит от $A$. Доказательство для $R$ аналогично.
Поскольку $O_A$ – точка пересечения прямых $PR$ и $QS$, а $\angle RO_AS= 90^{\circ}+\alpha$, получаем, что $O_A$ движется по дуге окружности, проходящей через $R$ и $S$.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь