Задача
Каждый отрезок с концами в вершинах правильного 100-угольника покрасили – в красный цвет, если между его концами четное число вершин, и в синий – в противном случае (в частности, все стороны 100-угольника красные). В вершинах расставили числа, сумма квадратов которых равна 1, а на отрезках – произведения чисел в концах. Затем из суммы чисел на красных отрезках вычли сумму чисел на синих. Какое наибольшее число могло получиться?
Решение
Обозначим числа в вершинах как x1, x2, ..., x100. Тогда сумма чисел на красных отрезках (обозначим ее за R) есть сумма всех попарных произведений чисел, стоящих на позициях с разной четностью:
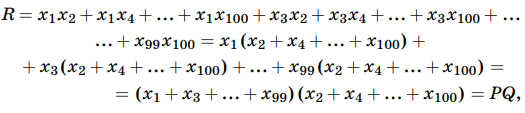
где P = x1 + x3 + ... + x99, а Q = x2 + x4 + ... + x100. Сумма на
синих отрезках (обозначим ее за B) есть сумма всех попарных произведений чисел, стоящих на позициях с одинаковой четностью: B = x1x3 + ... + x97x99 + x2x4 + ... + x98x100. Учитывая, что
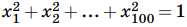, запишем, что
Искомая разность 
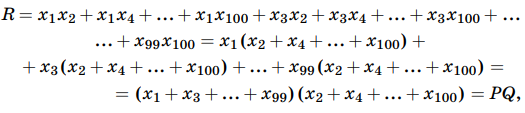Указанная оценка достигается, например, при x1 = x2 = ... = x100 =
1/10 или при 
Ответ
1/2.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь