Задача
Точка $O$ — центр описанной окружности треугольника $ABC$, $AH$ — его высота. Точка $P$ — основание перпендикуляра, опущенного из точки $A$ на прямую $CO$. Докажите, что прямая $HP$ проходит через середину отрезка $AB$.
Решение
Пусть $M$ — середина отрезка $AB$. Рассмотрим точки $A$, $O$, $M$ и $P$. Поскольку $\angle AMO=\angle APO =90^\circ$, точки $A$, $O$, $M$ и $P$ лежат на одной окружности. Значит, $\angle CPM=\angle OPM = \angle OAM$.
Рассмотрим точки $A$, $C$, $H$ и $P$. Они также лежат на одной окружности, так как $\angle AHC = \angle APC = 90^\circ$. Следовательно, $\angle CPH = \angle CAH$.
Помимо того, $$\angle CAH = 90^\circ - \angle ACB = 90^\circ - \frac{\angle AOB}{2} =90^\circ - \angle AOM = \angle OAM.$$ Получаем: $$\angle CPM = \angle OAM = \angle CAH = \angle CPH.$$ Значит, точки $M$, $P$ и $H$ лежат на одной прямой.
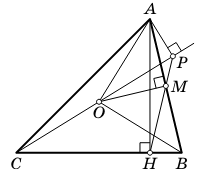Комментарий.Расположение точек может отличаться от представленного на
рисунке. Для других случаев расположения точек доказательство
аналогично.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь