Назад
Задача 166424 • Сложность: 2 • 7-9 класс
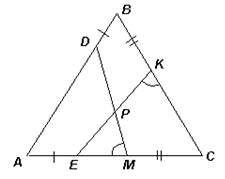
Задача

На сторонах AB и BC равностороннего треугольника ABC отмечены точки D и K соответственно, а на стороне AC отмечены точки E и M так, что DA + AE = KC + CM = AB. Отрезки DM и KE пересекаются. Найдите угол между ними.

Разделы:
Планиметрия
Источники:
Московская математическая регата Олимпиады и турниры 2017/2018 7 класс
Количество версий:
4
Решение

Рассмотрим треугольники ADM и CЕK (см. рисунок): DA = AB – AE = AC – AE = CE; AM = AC – CM = AB – CM = KC; ∠ DAM = 60° = ∠ EСK. Следовательно, эти треугольники равны (по двум сторонам и углу между ними). Тогда ∠ AMD = ∠ CKE.

Пусть прямые DM и KE пересекаются в точке Р. Из треугольника РЕМ: ∠ MPE = 180° – (∠ РЕМ + ∠ PME) = 180° – (∠ KЕC + ∠ CKE) = ∠ KCЕ = 60°.
Ответ

60°.

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет