Задача
Можно ли представить число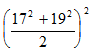 
в виде суммы квадратов двух натуральных чисел?
Решение
Первый способ. Пусть 18 = a. Тогда данное число можно записать и преобразовать так: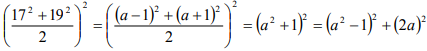 
.
Следовательно, 
.
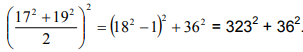Второй способ.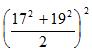 
= 3252 = (13·25)2 = 132·252 = 169·252 = (144 + 25)·252 = (122 + 52)·252 = 122·252 + 52·252 = 3002 + 1252.
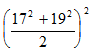Получив, что данное число равно 132252, можно продолжить иначе: = 132·252 = 132(202 + 152) = 132·202 + 132·152 = 2602 + 1952.
Третий способ. Так как 172 оканчивается цифрой 9, а 192 оканчивается цифрой 1, то число в скобках оканчивается цифрой 5. Значит, данное выражение имеет вид (5k)2, где k – некоторое натуральное число. Тогда положительный ответ на вопрос задачи следует из равенства: (5k)2 = (4k)2 + (3k)2.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь