Первый способ. Пусть I – центр вписанной окружности треугольника ABC, r – ее радиус, см. рисунок слева. Заметим, что ∠EID = ∠AIB = 135°, а CI = 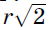(как диагональ квадрата со стороной r). Так как CI – диаметр окружности, описанной около треугольника EID, то по следствию из теоремы синусов DE = 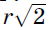sin∠EID = r.

Второй способ. Пусть прямые CE и CD пересекают AB в точках X и Y соответственно, см. рисунок справа. Тогда треугольник CBX – равнобедренный и CE = XE. Аналогично, CD = YD. Следовательно, DE – средняя линия треугольника XCY, то есть DE = 0,5XY.

В свою очередь, XY = BX + AY – AB = BC + AC – AB = 2r, откуда и следует утверждение задачи.

Комментарий. Точка I – центр описанной окружности треугольника XCY.

Ответ задачи отсутствует