Пусть W – середина дуги BC, не содержащей вершину A (см. рисунок). Тогда WC = WB, как равные хорды, стягивающие равные дуги. Рассмотрим точку M на стороне AB такую, что AM = AC. Тогда треугольники ACW и AMW равны по двум сторонам и углу между ними. Следовательно, WM = WC = WB, то есть треугольник BWM – равнобедренный.

Пусть прямая WM пересекает описанную окружность в точке N. Используя равенство вписанных углов и равенство углов при основании равнобедренного треугольника, получим: ∠ANM = ∠ANW = ∠ABW = ∠BMW = ∠AMN.

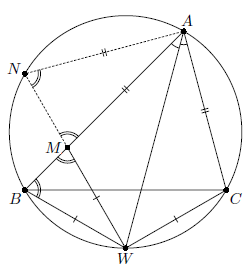
Следовательно, треугольник AMN – также равнобедренный и AN = AM = AC.

Отсюда вытекает следующий способ построения:

1. Построим окружность с центром A и радиусом AC. Пусть она пересекает сторону AB в точке M, а описанную окружность – в точке N.

2. Построим прямую MN. Точка пересечения этой прямой с описанной окружностью треугольника – искомая.

Ответ задачи отсутствует