Задача
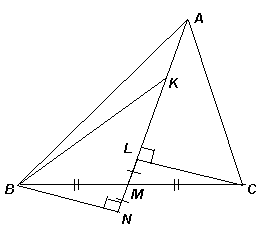
Точка M – середина стороны BC треугольника ABC. Из вершины C опущен перпендикуляр CL на прямую AM (L лежит между A и М). На отрезке AM отмечена точка K так, что AK = 2LM. Докажите, что ∠BKM = ∠CAM.
Решение
На продолжении отрезка LM отметим точку N так, что NM = LM (см. рисунок). Тогда треугольники CLM и BNM равны (по двум сторонам и углу между ними). Следовательно, ∠BNM = ∠CLM = 90° и BN = CL.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет