Задача
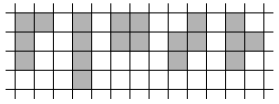
Фигурки из четырёх клеток называются тет- рамино. Они бывают пяти видов (см. рис.). Существует ли такая фигура, что при любом выборе вида тетрамино эту фигуру можно составить, используя тетраминошки только выбранного вида? (Переворачивать тетраминошки можно.)
Решение
Решение задачи отсутствует
Ответ
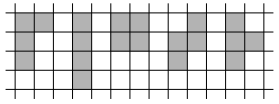
Да, существует, см. рисунок.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет