Задача
Постройте на координатной плоскости множество точек, удовлетворяющих равенству max {x, x²} + min {y, y²} = 1.
Решение
Заметим, что t > t² ⇔ 0 < t < 1. Поэтому требуется рассмотреть 4 случая.
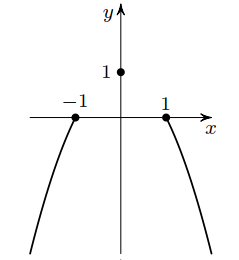
1) x ≤ 0 или x ≥ 1, y ≤ 0 или y ≥ 1. Тогда равенство примет вид x² + y = 1. При y > 1 оно выполняться не может, значит, графиком является часть параболы y = 1 – x², где y ≤ 0 или y = 1 (рис. слева).
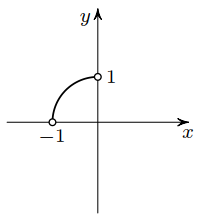
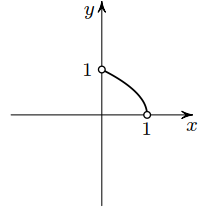
2) x ≤ 0 или x ≥ 1, 0 < y < 1. Тогда равенство примет вид x² + y² = 1. При x ≥ 1 равенство выполняться не может, значит, график – четверть окружности с выколотыми концами (рис. в центре).
Ответ
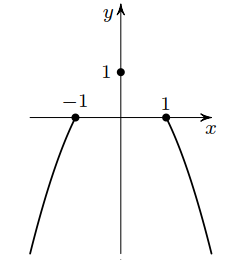
См. рис.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет