Задача
Лёша нарисовал геометрическую картинку, обведя четыре раза свой пластмассовый прямоугольный треугольник, прикладывая короткий катет к гипотенузе и совмещая вершину острого угла с вершиной прямого. Оказалось, что "замыкающий" пятый треугольник – равнобедренный (см. рис., равны именно отмеченные стороны). Найдите острые углы Лёшиного треугольника?
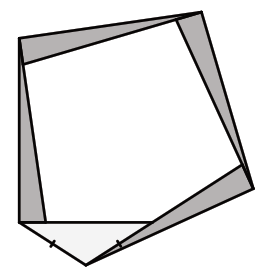
Решение
Пусть меньший из углов Лёшиного треугольника равен α. Обозначим точки так, как показано на рисунке.
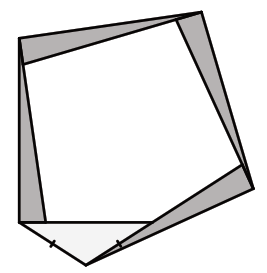
Ответ
90°/11, 900°/11.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет