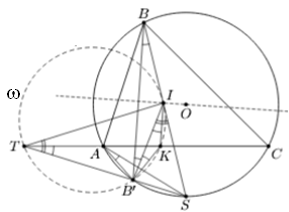
Пусть прямая BI вторично пересекает описанную окружность треугольника ABC в точке S, а лучи SB' и CA пересекаются в точке T (см. рис.). По лемме о трезубце (см. задачу 153119)  SA = SC = SI.  Из симметрии  ∠IB'B = ∠IBB' = φ.  Так как  OB = OB',  четырёхугольник AB'SB вписан, откуда  ∠SAB' = ∠SBB' = φ.  Заметим, что  ∠ATS = ∠СAS = ∠CBS – ∠ABB' = ∠ABS – ∠ABB' = ∠SBB' = φ.

  Таким образом, треугольникиSAB'иSTAподобны по двум углам, откуда  SB'·ST = SA² =SI².  Следовательно, прямаяSIкасается описанной окружности ω треугольникаTIB'. Поэтому  ∠ITB'= ∠B'IS= 2φ.  Значит,  ∠ITA= ∠ITB'– φ = φ.   Обозначим вторую точку пересечения окружности ω с прямойACчерезK.  ∠KB'I= ∠KTI= φ = ∠IB'B.  Также  ∠KIB'= ∠KTB'= φ = ∠IB'B.  Таким образом, прямыеKIиKB'касаются описанной окружности треугольникаBB'I, а точкаKлежит на прямойACпо построению.

Ответ задачи отсутствует