Задача
В остроугольном неравнобедренном треугольнике ABC проведены высоты AA1, BB1 и CC1. Пусть ω – его описанная окружность, точка M – середина стороны BC, P – вторая точка пересечения описанной окружности треугольника AB1C1 и ω, T – точка пересечения касательных к ω, проведённых в точках B и C, S – точка пересечения AT и ω. Докажите, что P, A1, S и середина отрезка MT лежат на одной прямой.
Решение
Пусть H – ортоцентр треугольника ABC, H' – точка, симметричная H относительно BC, X – точка, симметричная H относительно M, A' – середина дуги BC, не содержащей точку A, K – точка пересечения прямой AM и ω (см. рис.). Согласно задачам 155463 и 208949 точки H' и X лежат на ω. Кроме того, точка X диаметрально противоположна точке A (см. решение задачи 208600).
Согласно задаче 156983 AS – симедиана треугольника ABC. Поэтому дуги A'H' и A'X равны, значит, точки H' и X (как и точки S и K) симметричны относительно прямой MT. Лемма 1. Точки P, H, M и X лежат на одной прямой.
Доказательство. Заметим, что AH – диаметр описанной окружности треугольника AB1C1, то есть ∠APH = 90°. Точка X диаметрально противоположна точке A, поэтому и ∠APX = 90°, откуда и следует утверждение леммы. Лемма 2. Точки P, H' и T лежат на одной прямой.
Доказательство. Согласно задаче 56983 PT – симедиана треугольника BPC, а PM – его медиана. Поэтому достаточно доказать, что PH' и PM симметричны относительно биссектрисы угла BPC. Это следует из равенства дуг BH' и CX, которое фактически доказано выше.
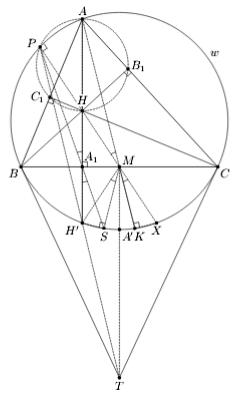
Поскольку точки P и A1 лежат на окружности с диаметром AM, то ∠H'MS = ∠XMK = ∠PMA = ∠PA1A. Кроме того, ∠MSH' = ∠MKX = ∠AKX = 90°. Следовательно, четырёхугольник A1H'SM – вписанный, откуда ∠PA1A = ∠H'MS = ∠H'A1S. Значит, точки P, A1 и S лежат на одной прямой.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь