Задача
Докажите, что окружность, построенная на стороне AB треугольника ABC как на диаметре, касается его вписанной окружности тогда и только тогда, когда сторона AB равна радиусу вневписанной окружности, касающейся этой стороны.
Решение
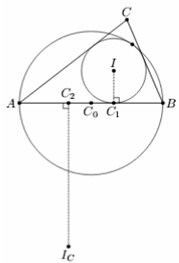
Пусть I и Ic – центры вписанной и вневписанной окружностей, r и rc – их радиусы, C1 и C2 – точки их касания со стороной AB, C0 – середина этой стороны, a, b и c – длины сторон треугольника, p – его полупериметр (см. рис.). Тогда AC1 = BC2 = p – a, BC1 = AC2 = p – b, C0C1 = C0C2 = |b–a|/2 (см. задачу 155483). Вписанная окружность касается окружности с диаметром AB тогда и только тогда, когда C0I1 = c/2 – r. По теореме Пифагора это эквивалентно равенству (c/2 – r)² = r² + (b–a/2)², то есть rc = (p – a)(p – b) = rrc (см. задачу 157600 а), откуда и следует утверждение задачи.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь