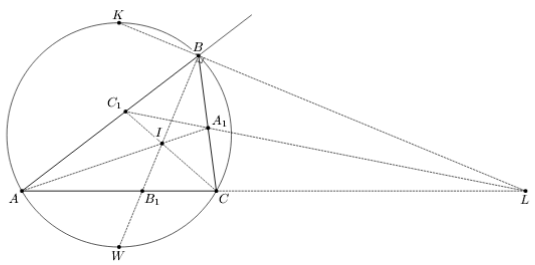
Пусть биссектрисы AA₁, BB₁ и CC₁ треугольника ABC пересекаются в точке I, BL – биссектриса внешнего угла B (L лежит на прямой AC, см. рис.).

  Заметим, что точки A₁, C₁ и L лежат на одной прямой (этот факт можно доказать, используя, например, теорему Менелая, или аналогично решению задачи 207770).

Отсюда вытекает способ построения.     1) Строим прямыеAI, BIиCI(биссектрисы углов треугольника) и находим точкиA₁,C₁и серединуWдугиACкак пересечениеBIс описанной окружностью.     2) Строим прямыеA₁C₁иACи находим точкуLих пересечения.     3) Строим прямуюBLи находим точкуKеё пересечения с окружностью.     4) ПроводимKW.   Так как уголKBW– прямой, тоKW– диаметр, что и требовалось.

Ответ задачи отсутствует