Задача
Два квадрата расположены, как показано на рисунке. Докажите, что площадь чёрного треугольника равна сумме площадей серых.
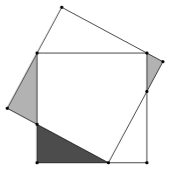
Решение
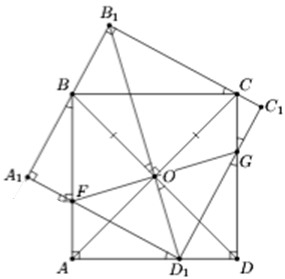
Пусть ABCD и A1B1C1D1 – данные квадраты, F – точка пересечения отрезков AB и A1D1, G – точка пересечения отрезков CD и C1D1, а O – центр квадрата ABCD (см. рис.).
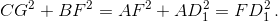 В силу очевидного подобия треугольниковCC1G, FA1BиFAD1отсюда следует утверждение задачи.
В силу очевидного подобия треугольниковCC1G, FA1BиFAD1отсюда следует утверждение задачи.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет