Задача
На стороне AB треугольника ABC отмечена точка K так, что AB = CK. Точки N и M – середины отрезков AK и BC соответственно. Отрезки NM и CK пересекаются в точке P. Докажите, что KN = KP.
Решение
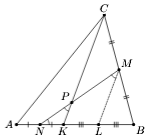
Пусть L – середина отрезка BK. Тогда ML – средняя линия треугольника BCK, то есть ML || CK и ML = ½ CK = ½ AB = LN. Следовательно, треугольник MLN равнобедренный. Из параллельности прямых ML и PK следует, что треугольник PKN подобен треугольнику MLN, значит, и он равнобедренный.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет