Задача
В выпуклом четырёхугольнике ABCD диагонали АС и BD равны, а серединный перпендикуляр к стороне ВС проходит через середину стороны AD.
Могут ли длины всех сторон четырёхугольника быть различными?
Решение
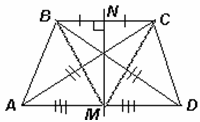
Пусть М и N – середины сторон AD и ВС соответственно. Тогда серединный перпендикуляр MN к отрезку ВС содержит медиану и высоту треугольника ВМС, значит, МВ = МС (см. рис.). Следовательно, треугольники АМС и DMB равны по трём сторонам. Поэтому ∠АМС = ∠DMB, а ∠DМС = ∠AMB (углы, смежные с равными). Значит, треугольники DМС и АМВ равны по двум сторонам и углу между ними, откуда DC = AB.
Ответ
Не могут.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет